Hypothesis and Procedure for its Testing

A hypothesis is an assumption about relations between variables. It is a tentative explanation of the research problem or a guess about the research outcome. Before starting the research, the researcher has a rather general, diffused, even confused notion of the problem. It may take long time for the researcher to say what questions he had been seeking answers to. Hence, an adequate statement about the research problem is very important. What is a good problem statement? It is an interrogative statement that asks: what relationship exists between two or more variables? It then further asks questions like: Is A related to B or not? How are A and B related to C? Is a related to B under conditions X and Y? Proposing a statement pertaining to relationship between A and B is called a hypothesis.

Procedure for Testing Hypothesis

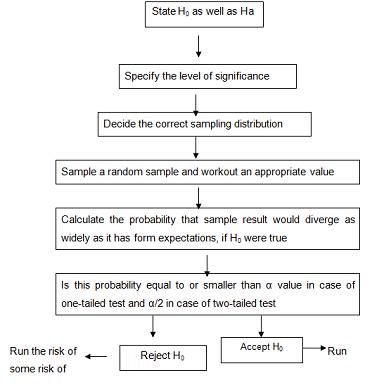
To test a hypothesis means to tell (on the basis of the data researcher has collected) whether or not the hypothesis seems to be valid. In hypothesis testing the main question is: whether the null hypothesis or not to accept the null hypothesis? Procedure for hypothesis testing refers to all those steps that we undertake for making a choice between the two actions i.e., rejection and acceptance of a null hypothesis. The various steps involved in hypothesis testing are stated below:

1) Making a Formal Statement

The step consists in making a formal statement of the null hypothesis (H_o) and also of the alternative hypothesis (H_a). This means that hypothesis should clearly state, considering the nature of the research problem. For instance, Mr. X of the Civil Engineering Department wants to test the load bearing capacity of an old bridge which must be more than 10 tons, in that case he can state his hypothesis as under:

Null hypothesis H_O: µ =10 tons

Alternative hypothesis H_a: µ >10 tons

Take another example. The average score in an aptitude test administered at the national level is 80. To evaluate a state’s education system, the average score of 100 of the state’s students selected on the random basis was 75. The state wants to know if there is a significance difference between the local scores and the national scores. In such a situation the hypothesis may be state as under:

Null hypothesis H_O: µ =80

Alternative hypothesis H_a: µ ‰  80

The formulation of hypothesis is an important step which must be accomplished with due care in accordance with the object and nature of the problem under consideration. It also indicates whether we should use a tailed test or a two tailed test. If ha is of the type greater than, we use alone tailed test, but when H_a is of the type “whether greater or smaller” then we use a two-tailed test.

2) Selecting a Significant Level

The hypothesis is tested on a pre-determined level of significance and such the same should have specified. Generally, in practice, either 5% level or 1% level is adopted for the purpose. The factors that affect the level of significance are:

• The magnitude of the difference between sample ;

• The size of the sample;
• The variability of measurements within samples;
• Whether the hypothesis is directional or non — directional (A directional hypothesis is one which predicts the direction of the difference between, say, means). In brief, the level of significance must be adequate in the context of the purpose and nature of inquiry.

3) Deciding the Distribution to Use

After deciding the level of significance, the next step in hypothesis testing is to determine the appropriate sampling distribution. The choice generally remains between distribution and the t distribution. The rules for selecting the correct distribution are similar to those which we have stated earlier in the context of estimation.

4) Selecting a Random Sample & Computing an Appropriate Value

Another step is to select a random sample(S) and compute an appropriate value from the sample data concerning the test statistic utilizing the relevant distribution. In other words, draw a sample to furnish empirical data.

5) Calculation of the Probability

One has then to calculate the probability that the sample result would diverge as widely as it has from expectations, if the null hypothesis were in fact true.

6) Comparing the Probability

Yet another step consists in comparing the probability thus calculated with the specified value for α, the significance level. If the calculated probability is equal to smaller than α value in case of one tailed test (and α/2 in case of two-tailed test), then reject the null hypothesis (i.e. accept the alternative hypothesis), but if the probability is greater than accept the null hypothesis. In case we reject H₀ we run a risk of (at most level of significance) committing an error of type I, but if we accept H₀, then we run some risk of committing error type II.

Flow Diagram for Testing Hypothesis

Source: Scribd.com