The standard error is an indispensable tool in the kit of a researcher, because it is used in testing the validity of statistical hypothesis. The standard deviation of the sampling distribution of a statistic is called the standard error. The standard error is important in dealing with statistics (measures of samples) which are normally distributed.
Here the use of the word “error” is justified in this connection by the fact that we usually regard the expected value to be true value and the divergence from it as error of estimation due to sampling fluctuations. The term standard error has a wider meaning than merely the standard deviation of simple sampling because of the following reasons;
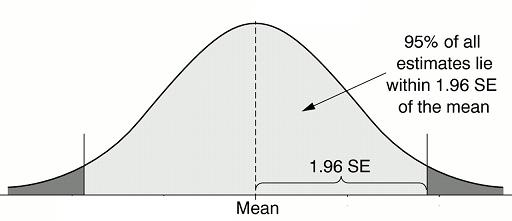
- The standard error is mainly employed for testing the validity of a given hypothesis. Mostly two levels of significance (0.05 and 0.01) are used for testing the validity of hypotheses. At 0.05 level of significance, if the difference between expected and observed values is more than 1.96 standard errors, the difference is considered significant. Such a difference could not have arisen due to sampling fluctuations but due to the operation of other causes. On the contrary, if this difference is less than 1.96 standard errors, it is considered not significant, arising due to sampling fluctuations. In this case, the result of an experiment supports the null hypothesis. Similarly at 0.01 level of significance if the differences between observed and expected values is more than 2.58 standard errors, the difference is considered significant. Such a difference could have arisen not due to sampling fluctuations but due to other causes. On the other hand if the difference is less than 2.58 standard errors, it may be attributed to sampling fluctuations and can be ignored. In this case, the result of the experiment supports the null hypothesis at 0.01 (1 %) level of significance.

- The standard error may fairly be taken to measure the unreliability of the sample estimate. The greater the standard error the greater the difference between observed and expected values and greater the unreliability of the sample estimate. On the other hand, the smaller value of the standard error, the smaller the difference between observed and expected values and greater the reliability of the sample estimate. The reciprocal of the standard error may be regarded as a measure of reliability. The reliability of an observed proportion varies as the square root of the number of observations on which it is based. The larger the sample size, the smaller the standard error and the smaller the sample size, the larger the standard error. In case, we want to double the precision the number of observations in the sample should be increased four times.
- The most important use of the standard errors is in the construction of confidence intervals within which parameter values are expected to fall. For a sufficiently large sample size, the sampling distribution tends to be normal. Therefore at 5% level of significance, the population mean is expected to lie within the interval of: X + 1.96 standard error of mean. Similarly at 1% level of significance, the population mean is expected to fall within the interval of: X + 2.58 standard error of mean. In the same way, other confidence intervals may be constructed.